Themes Unified State Exam codifier : free electromagnetic oscillations, oscillatory circuit, forced electromagnetic oscillations, resonance, harmonic electromagnetic oscillations.
Electromagnetic vibrations- These are periodic changes in charge, current and voltage that occur in an electrical circuit. The simplest system for observing electromagnetic oscillations is an oscillatory circuit.
Oscillatory circuit
Oscillatory circuit is a closed circuit formed by a capacitor and a coil connected in series.
Let's charge the capacitor, connect the coil to it and close the circuit. Will start to happen free electromagnetic oscillations- periodic changes in the charge on the capacitor and the current in the coil. Let us remember that these oscillations are called free because they occur without any external influence- only due to the energy stored in the circuit.
The period of oscillations in the circuit will be denoted, as always, by . We will assume the coil resistance to be zero.
Let us consider in detail all the important stages of the oscillation process. For greater clarity, we will draw an analogy with the oscillations of a horizontal spring pendulum.
Starting moment: . The capacitor charge is equal to , there is no current through the coil (Fig. 1). The capacitor will now begin to discharge.

Rice. 1.
Even though the coil resistance is zero, the current will not increase instantly. As soon as the current begins to increase, a self-induction emf will arise in the coil, preventing the current from increasing.
Analogy. The pendulum is pulled to the right by an amount and released at the initial moment. The initial speed of the pendulum is zero.
First quarter of the period: . The capacitor is discharged, its charge is this moment equal to . The current through the coil increases (Fig. 2).

Rice. 2.
The current increases gradually: the vortex electric field of the coil prevents the current from increasing and is directed against the current.
Analogy. The pendulum moves to the left towards the equilibrium position; the speed of the pendulum gradually increases. The deformation of the spring (aka the coordinate of the pendulum) decreases.
End of first quarter: . The capacitor is completely discharged. The current strength has reached its maximum value (Fig. 3). The capacitor will now begin recharging.

Rice. 3.
The voltage across the coil is zero, but the current will not disappear instantly. As soon as the current begins to decrease, a self-induction emf will arise in the coil, preventing the current from decreasing.
Analogy. The pendulum passes through its equilibrium position. Its speed reaches its maximum value. The spring deformation is zero.
Second quarter: . The capacitor is recharged - a charge of the opposite sign appears on its plates compared to what it was at the beginning (Fig. 4).

Rice. 4.
The current strength decreases gradually: the eddy electric field of the coil, supporting the decreasing current, is co-directed with the current.
Analogy. The pendulum continues to move to the left - from the equilibrium position to the right extreme point. Its speed gradually decreases, the deformation of the spring increases.
End of second quarter. The capacitor is completely recharged, its charge is again equal (but the polarity is different). The current strength is zero (Fig. 5). Now the reverse recharging of the capacitor will begin.

Rice. 5.
Analogy. The pendulum has reached the far right point. The speed of the pendulum is zero. The spring deformation is maximum and equal to .
Third quarter: . The second half of the oscillation period began; processes went into reverse direction. The capacitor is discharged (Fig. 6).

Rice. 6.
Analogy. The pendulum moves back: from the right extreme point to the equilibrium position.
End of the third quarter: . The capacitor is completely discharged. The current is maximum and again equal to , but this time it has a different direction (Fig. 7).

Rice. 7.
Analogy. The pendulum again passes through the equilibrium position at maximum speed, but this time in the opposite direction.
Fourth quarter: . The current decreases, the capacitor charges (Fig. 8).

Rice. 8.
Analogy. The pendulum continues to move to the right - from the equilibrium position to the extreme left point.
End of the fourth quarter and the entire period: . The reverse recharging of the capacitor is completed, the current is zero (Fig. 9).

Rice. 9.
This moment is identical to the moment, and this figure is identical to Figure 1. One complete oscillation took place. Now the next oscillation will begin, during which the processes will occur exactly as described above.
Analogy. The pendulum returned to its original position.
The considered electromagnetic oscillations are undamped- they will continue indefinitely. After all, we assumed that the coil resistance is zero!
In the same way, the oscillations of a spring pendulum will be undamped in the absence of friction.
In reality, the coil has some resistance. Therefore, the oscillations in a real oscillatory circuit will be damped. So, after one complete oscillation, the charge on the capacitor will be less than the original value. Over time, the oscillations will completely disappear: all the energy initially stored in the circuit will be released in the form of heat at the resistance of the coil and connecting wires.
In the same way, the oscillations of a real spring pendulum will be damped: all the energy of the pendulum will gradually turn into heat due to the inevitable presence of friction.
Energy transformations in an oscillatory circuit
We continue to consider undamped oscillations in the circuit, considering the coil resistance to be zero. The capacitor has a capacitance and the inductance of the coil is equal to .
Since there are no heat losses, energy does not leave the circuit: it is constantly redistributed between the capacitor and the coil.
Let's take a moment in time when the charge of the capacitor is maximum and equal to , and there is no current. The energy of the magnetic field of the coil at this moment is zero. All the energy of the circuit is concentrated in the capacitor:
Now, on the contrary, let’s consider the moment when the current is maximum and equal to , and the capacitor is discharged. The energy of the capacitor is zero. All the circuit energy is stored in the coil:
At an arbitrary moment in time, when the charge of the capacitor is equal and current flows through the coil, the energy of the circuit is equal to:
Thus,
(1)
Relationship (1) is used to solve many problems.
Electromechanical analogies
In the previous leaflet about self-induction, we noted the analogy between inductance and mass. Now we can establish several more correspondences between electrodynamic and mechanical quantities.
For a spring pendulum we have a relationship similar to (1):
(2)
Here, as you already understood, is the spring stiffness, is the mass of the pendulum, and is the current values of the coordinates and speed of the pendulum, and is their greatest values.
Comparing equalities (1) and (2) with each other, we see the following correspondences:
(3)
(4)
(5)
(6)
Based on these electromechanical analogies, we can foresee a formula for the period of electromagnetic oscillations in an oscillatory circuit.
In fact, the period of oscillation of a spring pendulum, as we know, is equal to:
In accordance with analogies (5) and (6), here we replace mass with inductance, and stiffness with inverse capacitance. We get:
(7)
Electromechanical analogies do not fail: formula (7) gives the correct expression for the period of oscillations in the oscillatory circuit. It is called Thomson's formula. We will present its more rigorous conclusion shortly.
Harmonic law of oscillations in a circuit
Recall that oscillations are called harmonic, if the oscillating quantity changes over time according to the law of sine or cosine. If you have forgotten these things, be sure to repeat the “Mechanical Vibrations” sheet.
The oscillations of the charge on the capacitor and the current in the circuit turn out to be harmonic. We will prove this now. But first we need to establish rules for choosing the sign for the capacitor charge and for the current strength - after all, when oscillating, these quantities will take on both positive and negative values.
First we choose positive bypass direction contour. The choice does not matter; let this be the direction counterclock-wise(Fig. 10).

Rice. 10. Positive bypass direction
The current strength is considered positive class="tex" alt="(I > 0)"> , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной .!}
The charge on a capacitor is the charge on its plate to which positive current flows (i.e., the plate to which the bypass direction arrow points). In this case - charge left capacitor plates.
With such a choice of signs of current and charge, the following relation is valid: (with a different choice of signs it could happen). Indeed, the signs of both parts coincide: if class="tex" alt="I > 0"> , то заряд левой пластины возрастает, и потому !} class="tex" alt="\dot(q) > 0"> !}.
The quantities and change over time, but the energy of the circuit remains unchanged:
(8)
Therefore, the derivative of energy with respect to time becomes zero: . We take the time derivative of both sides of relation (8); do not forget that complex functions are differentiated on the left (If is a function of , then according to the rule of differentiation of complex functions, the derivative of the square of our function will be equal to: ):
Substituting and here, we get:
But the current strength is not a function that is identically equal to zero; That's why
Let's rewrite this as:
(9)
We have obtained a differential equation of harmonic oscillations of the form , where . This proves that the charge on the capacitor oscillates according to a harmonic law (i.e., according to the law of sine or cosine). The cyclic frequency of these oscillations is equal to:
(10)
This quantity is also called natural frequency contour; It is with this frequency that free (or, as they also say, own fluctuations). The oscillation period is equal to:
We again come to Thomson's formula.
The harmonic dependence of charge on time in the general case has the form:
(11)
The cyclic frequency is found by formula (10); the amplitude and initial phase are determined from the initial conditions.
We will look at the situation discussed in detail at the beginning of this leaflet. Let the charge of the capacitor be maximum and equal (as in Fig. 1); there is no current in the circuit. Then the initial phase is , so that the charge varies according to the cosine law with amplitude:
(12)
Let's find the law of change in current strength. To do this, we differentiate relation (12) with respect to time, again not forgetting about the rule for finding the derivative of a complex function:
We see that the current strength also changes according to a harmonic law, this time according to the sine law:
(13)
The amplitude of the current is:
The presence of a “minus” in the law of current change (13) is not difficult to understand. Let's take, for example, a time interval (Fig. 2).
The current flows in the negative direction: . Since , the oscillation phase is in the first quarter: . The sine in the first quarter is positive; therefore, the sine in (13) will be positive on the time interval under consideration. Therefore, to ensure that the current is negative, the minus sign in formula (13) is really necessary.
Now look at fig. 8 . The current flows in the positive direction. How does our “minus” work in this case? Figure out what's going on here!
Let us depict graphs of charge and current fluctuations, i.e. graphs of functions (12) and (13). For clarity, let us present these graphs in the same coordinate axes (Fig. 11).

Rice. 11. Graphs of charge and current fluctuations
Please note: charge zeros occur at current maxima or minima; conversely, current zeros correspond to charge maxima or minima.
Using the reduction formula
Let us write the law of current change (13) in the form:
Comparing this expression with the law of charge change, we see that the current phase, equal to, is greater than the charge phase by an amount. In this case they say that the current ahead in phase charge on ; or phase shift between current and charge is equal to ; or phase difference between current and charge is equal to .
The advance of the charge current in phase is graphically manifested in the fact that the current graph is shifted left on relative to the charge graph. The current strength reaches, for example, its maximum a quarter of a period earlier than the charge reaches its maximum (and a quarter of a period exactly corresponds to the phase difference).
Forced electromagnetic oscillations
As you remember, forced oscillations arise in the system under the influence of a periodic forcing force. The frequency of forced oscillations coincides with the frequency of the driving force.
Forced electromagnetic oscillations will occur in a circuit connected to a sinusoidal voltage source (Fig. 12).

Rice. 12. Forced vibrations
If the source voltage changes according to the law:
then oscillations of charge and current occur in the circuit with a cyclic frequency (and with a period, respectively). The AC voltage source seems to “impose” its oscillation frequency on the circuit, making you forget about its own frequency.
The amplitude of forced oscillations of charge and current depends on frequency: the amplitude is greater, the closer to the natural frequency of the circuit. When resonance- a sharp increase in the amplitude of oscillations. We'll talk about resonance in more detail in the next worksheet on alternating current.
Lesson No. 48-169 Oscillatory circuit. Free electromagnetic oscillations. Conversion of energy in an oscillatory circuit. Thompson's formula.Oscillations- movements or states that repeat over time.Electromagnetic vibrations -these are electrical vibrations andmagnetic fields that resistdriven by periodic infidelitycharge, current and voltage. An oscillatory circuit is a system consisting of an inductor and a capacitor(Fig. a). If the capacitor is charged and shorted to the coil, then current will flow through the coil (Fig. b). When the capacitor is discharged, the current in the circuit will not stop due to self-induction in the coil. The induction current, in accordance with Lenz's rule, will flow in the same direction and recharge the capacitor (Fig. c). The current in this direction will stop, and the process will repeat in the opposite direction (Fig. G).
Thus, in fluctuationstelny contour of the originelectromagnetic oscillationsnia due to energy conversionelectric field condensationra( W E =  )
into the energy of the magnetic field of a coil with current(W M =
)
into the energy of the magnetic field of a coil with current(W M =  ),
and vice versa.
),
and vice versa.
Harmonic oscillations are periodic changes in a physical quantity depending on time, occurring according to the law of sine or cosine.
 The equation describing free electromagnetic oscillations takes the form
The equation describing free electromagnetic oscillations takes the form
q"= - ω 0 2 q (q" is the second derivative.
Main characteristics of oscillatory motion:
The period of oscillation is the minimum period of time T after which the process is completely repeated.
The amplitude of harmonic oscillations is the modulus of the largest value of the oscillating quantity.
Knowing the period, you can determine the frequency of oscillations, i.e. the number of oscillations per unit of time, for example per second. If one oscillation occurs in time T, then the number of oscillations in 1 s ν is determined as follows: ν = 1/T.
Recall that in the International System of Units (SI), the frequency of oscillations is equal to one if one oscillation occurs in 1 s. The unit of frequency is called the hertz (abbreviated: Hz) after the German physicist Heinrich Hertz.
After a period of time equal to the period T, i.e., when the cosine argument increases by ω 0
T, the charge value is repeated and the cosine takes on its previous value. From the mathematics course we know that the smallest period of the cosine is 2n. Therefore, ω 0
T=2π, whence ω 0
= 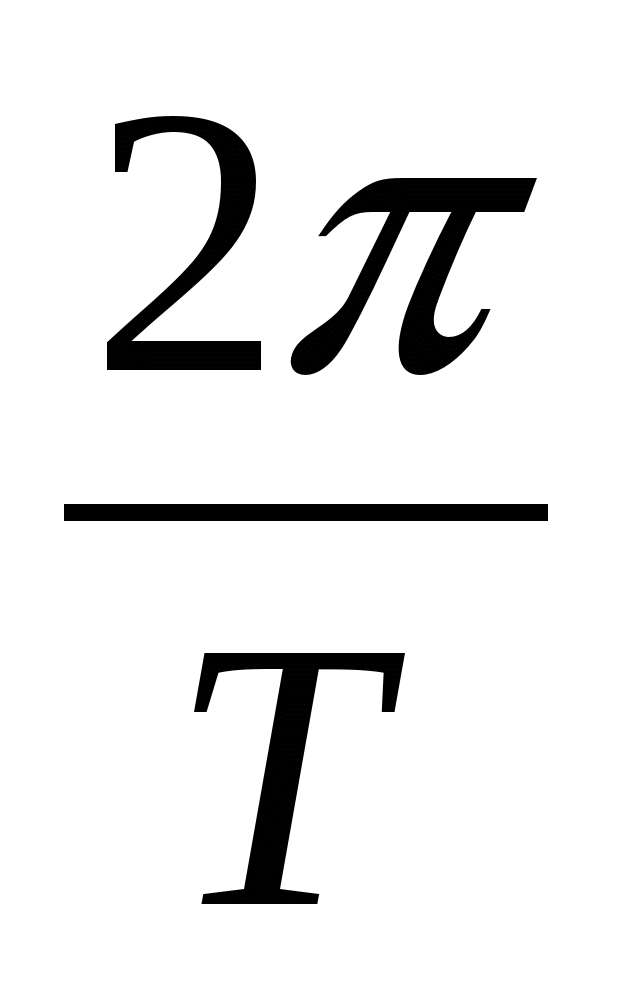 =2πν Thus, the value ω 0
- this is the number of oscillations, but not in 1 s, but in 2 s. It is called cyclical or circular frequency.
=2πν Thus, the value ω 0
- this is the number of oscillations, but not in 1 s, but in 2 s. It is called cyclical or circular frequency.
The frequency of free oscillations is called natural vibrational frequencysystems. Often in the following, for brevity, we will simply refer to the cyclic frequency as the frequency. Distinguish cyclic frequency ω 0 from frequency ν can be used according to the notation.
By analogy with the solution of the differential equation for a mechanical oscillatory system cyclic frequency of free electricitysky fluctuations is equal to:ω 0 = 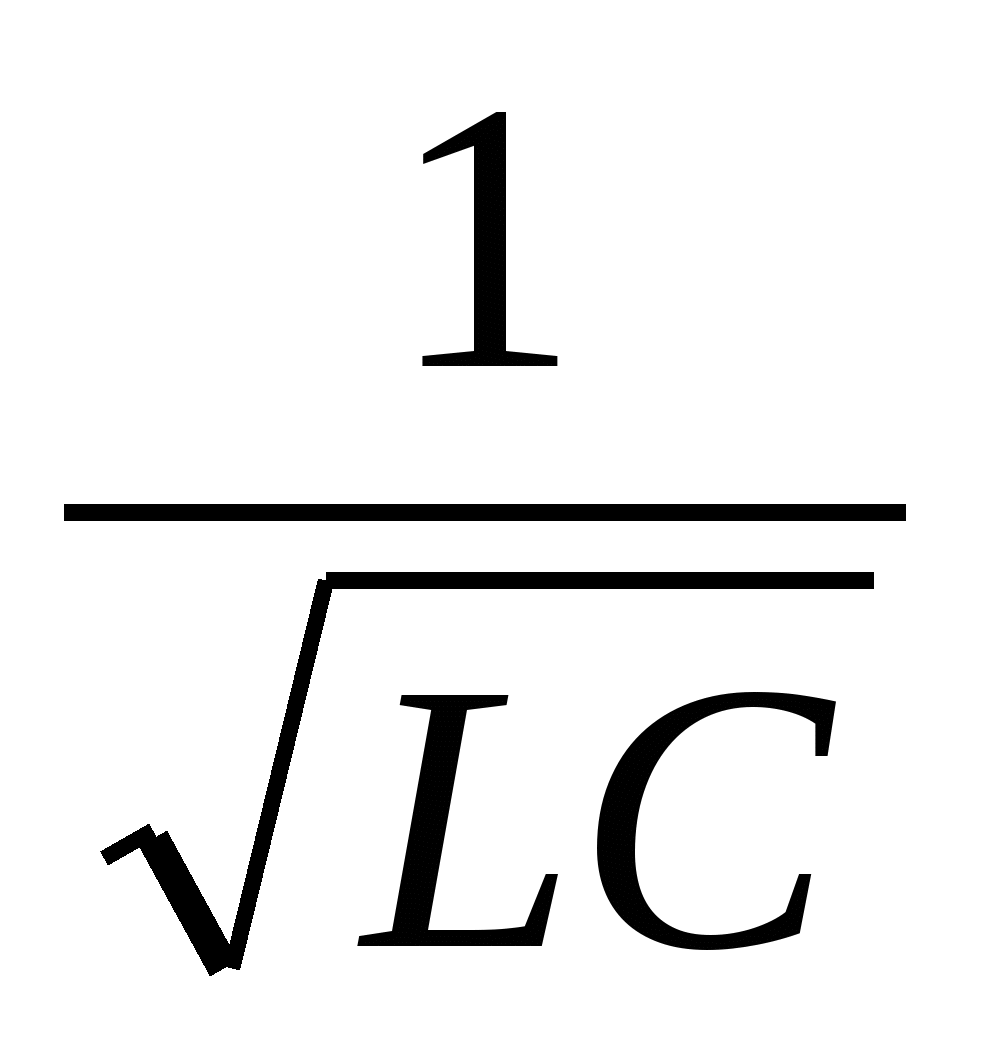
The period of free oscillations in the circuit is equal to: T=  =2π
=2π  - Thomson's formula.
- Thomson's formula.
Oscillation phase (from Greek word phasis - appearance, stage of development of a phenomenon) - the value φ, standing under the sign of cosine or sine. The phase is expressed in angular units - radians. The phase determines, for a given amplitude, the state of the oscillatory system at any time.
Oscillations with the same amplitudes and frequencies may differ from each other in phases.
Since ω 0
= , then φ= ω 0
Т=2π . The ratio shows how much of the period has passed since the start of the oscillation. Any time value expressed in fractions of a period corresponds to a phase value expressed in radians. So, after time t=
. The ratio shows how much of the period has passed since the start of the oscillation. Any time value expressed in fractions of a period corresponds to a phase value expressed in radians. So, after time t= 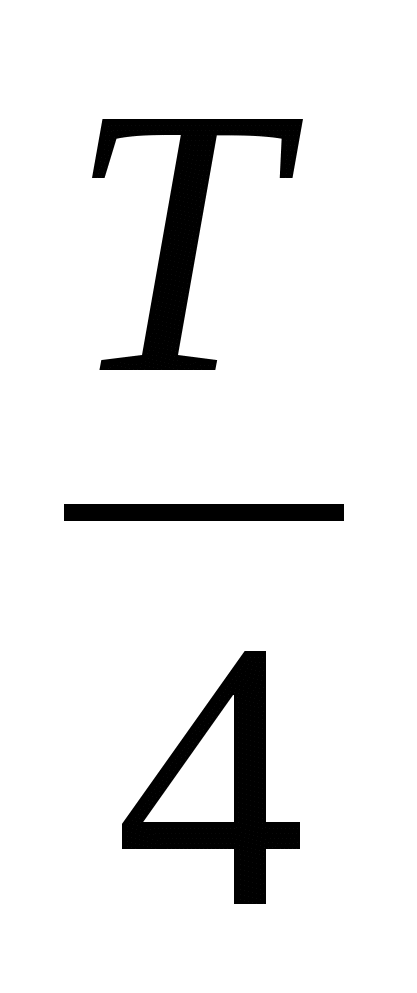 (quarter period) φ=
(quarter period) φ= 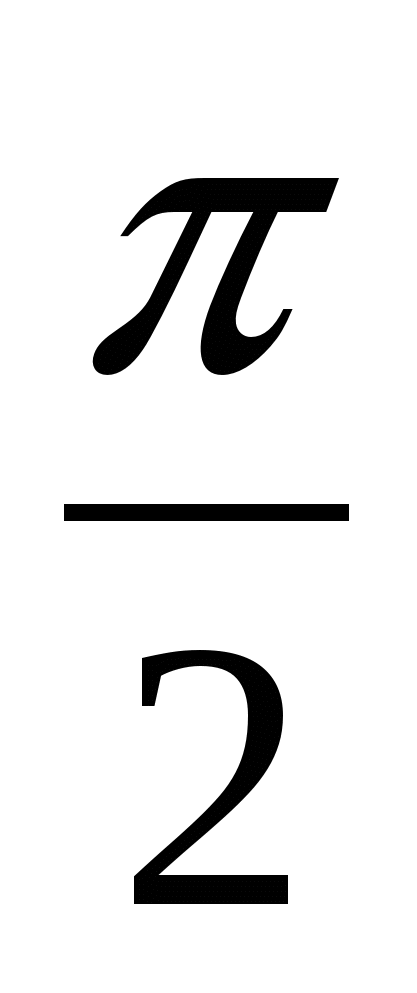 , after half the period φ = π, after the whole period φ = 2π, etc. You can plot the dependence
, after half the period φ = π, after the whole period φ = 2π, etc. You can plot the dependence
 charge does not depend on time, but on phase. The figure shows the same cosine wave as the previous one, but on the horizontal axis they are plotted instead of time
charge does not depend on time, but on phase. The figure shows the same cosine wave as the previous one, but on the horizontal axis they are plotted instead of time
different meanings phase φ.
Correspondence between mechanical and electrical quantities in oscillatory processes
Mechanical quantities
Tasks.942(932). The initial charge imparted to the capacitor of the oscillatory circuit was reduced by 2 times. How many times did: a) voltage amplitude change; b) current amplitude;
c) the total energy of the electric field of the capacitor and the magnetic field of the coil?
943(933). With an increase in the voltage on the capacitor of the oscillatory circuit by 20 V, the amplitude of the current increased by 2 times. Find the initial voltage.
945(935). The oscillatory circuit consists of a capacitor with a capacity C = 400 pF and an inductance coil L = 10 mH. Find the amplitude of current I oscillations T , if the amplitude of voltage fluctuations U T = 500 V.
952(942). After what time (in fractions of the period t/T) for the first time there will be a charge on the capacitor of the oscillating circuit equal to half the amplitude value?
957(947). What inductance coil should be included in the oscillatory circuit in order to obtain a free oscillation frequency of 10 MHz with a capacitor capacitance of 50 pF?
Oscillatory circuit. Period of free oscillations.
1. After the capacitor of the oscillating circuit has been given a charge q = 10 -5 C, damped oscillations arose in the circuit. How much heat will be released in the circuit by the time the oscillations in it completely die out? Capacitance of the capacitor C = 0.01 μF.
2. The oscillating circuit consists of a capacitor with a capacity of 400 nF and a coil with an inductance of 9 μH. What is the period of natural oscillation of the circuit?
3. What inductance must be included in the oscillatory circuit in order to obtain a natural oscillation period of 2∙ 10 -6 s with a capacitance of 100 pF.
4. Compare spring stiffness k1/k2 of two pendulums with masses of loads of 200g and 400g, respectively, if the periods of their oscillations are equal.
5. Under the action of a stationary load hanging on a spring, its elongation was equal to 6.4 cm. Then the weight was pulled back and released, as a result of which it began to oscillate. Determine the period of these oscillations.
6. A load was suspended from a spring, brought out of its equilibrium position and released. The load began to oscillate with a period of 0.5 s. Determine the elongation of the spring after the oscillations stop. Ignore the mass of the spring.
7. During the same time, one mathematical pendulum makes 25 oscillations, and the other 15. Find their lengths if one of them is 10 cm shorter than the other.8. The oscillatory circuit consists of a capacitor with a capacity of 10 mF and an inductor of 100 mH. Find the amplitude of voltage fluctuations if the amplitude of current fluctuations is 0.1A9. The inductance of the oscillating circuit coil is 0.5 mH. It is required to configure this circuit to a frequency of 1 MHz. What should be the capacitance of the capacitor in this circuit?Exam questions:
1. Which of the following expressions determines the period of free oscillations in an oscillatory circuit? A.; B.  ; IN.
; IN. 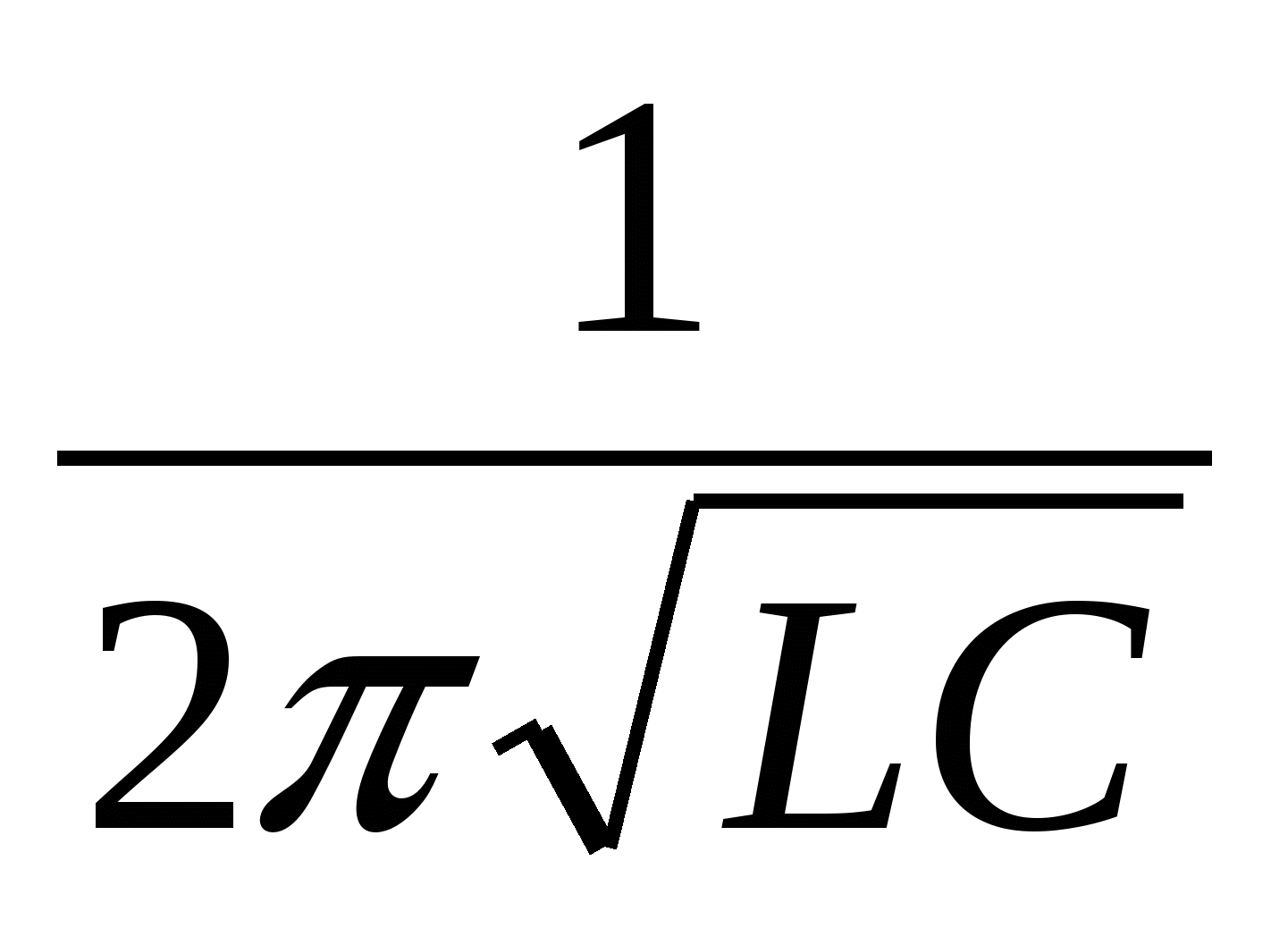 ; G.
; G.  ; D. 2 .
; D. 2 .
2 . Which of the following expressions determines the cyclic frequency of free oscillations in an oscillatory circuit? A.B.
. Which of the following expressions determines the cyclic frequency of free oscillations in an oscillatory circuit? A.B.  IN.
IN.  G.
G.  D. 2π
D. 2π
3. The figure shows a graph of the X coordinate of a body performing harmonic oscillations along the x axis as a function of time. What is the period of vibration of the body?
A. 1 s; B. 2 s; V. 3 s . G. 4 p.
4. The figure shows the wave profile at a certain point in time. What is its length?
A. 0.1 m. B. 0.2 m. C. 2 m. D. 4 m. D. 5 m.5
 . The figure shows a graph of the current through the oscillating circuit coil versus time. What is the period of current oscillation? A. 0.4 s. B. 0.3 s. V. 0.2 s. G. 0.1 s.
. The figure shows a graph of the current through the oscillating circuit coil versus time. What is the period of current oscillation? A. 0.4 s. B. 0.3 s. V. 0.2 s. G. 0.1 s. D. There is no correct answer among answers A-D.

6. The figure shows the wave profile at a certain point in time. What is its length?
A. 0.2 m. B. 0.4 m. C. 4 m. D. 8 m. D. 12 m.
7. Electrical oscillations in the oscillatory circuit are given by the equation q =10 -2 ∙ cos 20t (Cl).
What is the amplitude of charge oscillations?
A . 10 -2 Cl. B.cos 20t Cl. B.20t Cl. G.20 Cl. D. Among the answers A-D there is no correct one.
8. During harmonic vibrations along the OX axis, the coordinate of the body changes according to the law X=0.2cos(5t+  ). What is the amplitude of the body's vibrations?
). What is the amplitude of the body's vibrations?
A. Xm; B. 0.2 m; V. сos(5t+) m; (5t+)m; D.m
9. Oscillation frequency of the wave source is 0.2 s -1 wave propagation speed is 10 m/s. What is the wavelength? A. 0.02 m. B. 2 m. C. 50 m.
D. According to the conditions of the problem, it is impossible to determine the wavelength. D. There is no correct answer among answers A-D.
10. Wave length 40 m, propagation speed 20 m/s. What is the oscillation frequency of the wave source?
A. 0.5 s -1 . B. 2 s -1 . V. 800 s -1 .
D. According to the conditions of the problem, it is impossible to determine the oscillation frequency of the wave source.
D. There is no correct answer among answers A-D.
3
An electromagnetic field can exist in the absence of electric charges or currents: it is precisely such “self-sustaining” electric and magnetic fields that constitute electromagnetic waves, which include visible light, infrared, ultraviolet and x-ray radiation, radio waves, etc.
§ 25. Oscillatory circuit
The simplest system in which natural electromagnetic oscillations are possible is the so-called oscillatory circuit, consisting of a capacitor and an inductor connected to each other (Fig. 157). Like a mechanical oscillator, for example a massive body on an elastic spring, natural oscillations in the circuit are accompanied by energy transformations.
Rice. 157. Oscillatory circuit
Analogy between mechanical and electromagnetic vibrations. For an oscillatory circuit, an analogue of the potential energy of a mechanical oscillator (for example, the elastic energy of a deformed spring) is the energy of the electric field in a capacitor. An analogue of the kinetic energy of a moving body is the energy of the magnetic field in an inductor. In fact, the energy of the spring is proportional to the square of the displacement from the equilibrium position and the energy of the capacitor is proportional to the square of the charge. The kinetic energy of a body is proportional to the square of its speed and the energy of the magnetic field in the coil is proportional to the square of the current.
The total mechanical energy of the spring oscillator E is equal to the sum of the potential and kinetic energies:
![]()
Energy of vibrations. Similarly, the total electromagnetic energy of the oscillatory circuit is equal to the sum of the energies of the electric field in the capacitor and the magnetic field in the coil:
![]()
From a comparison of formulas (1) and (2) it follows that the analogue of the stiffness k of a spring oscillator in an oscillatory circuit is the reciprocal of the capacitance C, and the analogue of mass is the inductance of the coil
Let us recall that in a mechanical system, the energy of which is given by expression (1), its own undamped harmonic oscillations can occur. The square of the frequency of such oscillations is equal to the ratio of the coefficients of the squares of displacement and speed in the expression for energy:
Natural frequency. In an oscillatory circuit, the electromagnetic energy of which is given by expression (2), its own undamped harmonic oscillations can occur, the square of the frequency of which is also, obviously, equal to the ratio of the corresponding coefficients (i.e., the coefficients for the squares of charge and current):
From (4) follows an expression for the oscillation period, called Thomson’s formula:
![]()
During mechanical oscillations, the dependence of the displacement x on time is determined by a cosine function, the argument of which is called the oscillation phase:
Amplitude and initial phase. The amplitude A and the initial phase a are determined by the initial conditions, i.e., the values of displacement and velocity at
Similarly, with electromagnetic natural oscillations in the circuit, the charge of the capacitor depends on time according to the law
where the frequency is determined, in accordance with (4), only by the properties of the circuit itself, and the amplitude of charge oscillations and the initial phase a, like that of a mechanical oscillator, are determined
initial conditions, i.e., the values of the capacitor charge and current strength at Thus, the natural frequency does not depend on the method of excitation of oscillations, while the amplitude and initial phase are determined precisely by the excitation conditions.
Energy transformations. Let us consider in more detail energy transformations during mechanical and electromagnetic vibrations. In Fig. 158 schematically depicts the states of mechanical and electromagnetic oscillators at time intervals of a quarter period

Rice. 158. Energy transformations during mechanical and electromagnetic vibrations
Twice during the oscillation period, energy is converted from one type to another and back again. The total energy of the oscillatory circuit, like the total energy of a mechanical oscillator, remains unchanged in the absence of dissipation. To verify this, you need to substitute expression (6) for and expression for the current into formula (2)
Using formula (4) for we obtain

Rice. 159. Graphs of the dependence of the energy of the electric field of the capacitor and the energy of the magnetic field in the coil on the time of charging the capacitor
The constant total energy coincides with the potential energy at the moments when the charge on the capacitor is maximum, and coincides with the energy of the magnetic field of the coil - the "kinetic" energy - at the moments when the charge on the capacitor becomes zero and the current is maximum. During mutual transformations, two types of energy perform harmonic vibrations with the same amplitude, out of phase with each other and with a frequency relative to their average value. This can be easily seen from Fig. 158, and using formulas for trigonometric functions of half an argument:
Graphs of the dependence of the electric field energy and magnetic field energy on the charging time of the capacitor are shown in Fig. 159 for the initial phase
Quantitative laws of natural electromagnetic oscillations can be established directly on the basis of the laws for quasi-stationary currents, without resorting to an analogy with mechanical oscillations.
Equation for oscillations in a circuit. Let's consider the simplest oscillatory circuit shown in Fig. 157. When going around the circuit, for example, counterclockwise, the sum of the voltages on the inductor and capacitor in such a closed series circuit is zero:
![]()
The voltage on the capacitor is related to the charge of the plate and to the capacitance With the relation The voltage on the inductance at any moment of time is equal in magnitude and opposite in sign to the self-inductive emf, therefore the Current in the circuit is equal to the rate of change of the charge of the capacitor: Substituting the current strength in the expression for the voltage on the inductor and denoting the second derivative of the capacitor charge with respect to time through
We obtain Now expression (10) takes the form
![]()
Let's rewrite this equation differently, introducing by definition:
![]()
Equation (12) coincides with the equation of harmonic oscillations of a mechanical oscillator with a natural frequency. The solution to such an equation is given by a harmonic (sinusoidal) time function (6) with arbitrary values of the amplitude and initial phase a. This implies all the above results regarding electromagnetic oscillations in the circuit.
Attenuation of electromagnetic oscillations. So far, natural vibrations in an idealized mechanical system and an idealized LC circuit have been discussed. The idealization consisted of neglecting friction in the oscillator and electrical resistance in the circuit. Only in this case will the system be conservative and the oscillation energy will be conserved.

Rice. 160. Oscillatory circuit with resistance
The dissipation of oscillation energy in the circuit can be taken into account in the same way as was done in the case of a mechanical oscillator with friction. The presence of electrical resistance of the coil and connecting wires is inevitably associated with the release of Joule heat. As before, this resistance can be considered as an independent element in the electrical circuit of the oscillatory circuit, considering the coil and wires ideal (Fig. 160). When considering a quasi-stationary current in such a circuit, the voltage across the resistance must be added to equation (10)
Substituting in we get
Introducing designations
we rewrite equation (14) in the form
Equation (16) for has exactly the same form as the equation for when a mechanical oscillator oscillates with
friction proportional to speed (viscous friction). Therefore, in the presence of electrical resistance in the circuit, electromagnetic oscillations occur according to the same law as the mechanical oscillations of an oscillator with viscous friction.
Dissipation of vibration energy. As with mechanical vibrations, it is possible to establish the law of the decrease in energy of natural vibrations over time by applying the Joule-Lenz law to calculate the heat released:
![]()
As a result, in the case of small attenuation for time intervals much larger than the oscillation period, the rate of decrease in the oscillation energy turns out to be proportional to the energy itself:
![]()
The solution to equation (18) has the form
The energy of natural electromagnetic oscillations in a circuit with resistance decreases according to an exponential law.
The energy of oscillations is proportional to the square of their amplitude. For electromagnetic oscillations this follows, for example, from (8). Therefore, the amplitude of damped oscillations, in accordance with (19), decreases according to the law
Lifetime of oscillations. As can be seen from (20), the amplitude of the oscillations decreases by a factor of a time equal to, regardless of the initial value of the amplitude. This time x is called the lifetime of the oscillations, although, as can be seen from (20), the oscillations formally continue indefinitely. In reality, of course, it makes sense to talk about oscillations only as long as their amplitude exceeds characteristic meaning the level of thermal noise in a given circuit. Therefore, in fact, the oscillations in the circuit “live” for a finite time, which, however, can be several times greater than the lifetime x introduced above.
It is often important to know not the lifetime of oscillations x itself, but the number of complete oscillations that will occur in the circuit during this time x. This number multiplied by is called the circuit quality factor.
Strictly speaking, damped oscillations are not periodic. With low attenuation, we can conditionally speak of a period, which is understood as the time interval between two
successive maximum values of the capacitor charge (same polarity), or maximum current values (one direction).
Damping of oscillations affects the period, causing it to increase compared to the idealized case of no damping. With low damping, the increase in the oscillation period is very small. However, with strong attenuation, there may be no oscillations at all: the charged capacitor will discharge aperiodically, i.e., without changing the direction of the current in the circuit. This will happen when i.e. when
Exact solution. The patterns of damped oscillations formulated above follow from the exact solution of differential equation (16). By direct substitution we can verify that it has the form
where are arbitrary constants, the values of which are determined from the initial conditions. With low damping, the cosine multiplier can be considered as a slowly varying amplitude of oscillations.
Task
Recharging capacitors through an inductor. In the circuit, the diagram of which is shown in Fig. 161, the charge of the upper capacitor is equal and the lower one is not charged. At the moment the key is closed. Find the dependence of the charging time of the upper capacitor and the current in the coil.

Rice. 161. At the initial moment of time, only one capacitor is charged

Rice. 162. Charges of capacitors and current in the circuit after closing the key

Rice. 163. Mechanical analogy for the electrical circuit shown in Fig. 162
Solution. After the key is closed, oscillations occur in the circuit: the upper capacitor begins to discharge through the coil, while charging the lower one; then everything happens in the opposite direction. Let, for example, at be the upper plate of the capacitor is positively charged. Then
after a short period of time, the signs of the charges of the capacitor plates and the direction of the current will be as shown in Fig. 162. Let us denote by the charges those plates of the upper and lower capacitors that are connected to each other through an inductor. Based on the law of conservation of electric charge
The sum of the voltages on all elements of the closed loop at each moment of time is zero:
![]()
The sign of the voltage on the capacitor corresponds to the charge distribution in Fig. 162. and the indicated direction of the current. The expression for the current through the coil can be written in either of two forms:
![]()
Let us exclude from the equation using relations (22) and (24):
![]()
Introducing designations
![]()
Let's rewrite (25) in the following form:
![]()
If instead of entering the function
![]()
and take into account that then (27) takes the form
![]()
This is the usual equation of undamped harmonic oscillations, which has a solution
where and are arbitrary constants.
Returning from the function, we obtain the following expression for the dependence of the charging time of the upper capacitor:
To determine the constants and a, we take into account that at the initial moment the charge and current For the current strength from (24) and (31) we have
Since it follows that Substituting now in and taking into account that we get
![]()
So, the expressions for charge and current have the form

The nature of charge and current oscillations is especially clear when the capacitor capacitances are the same. In this case

The charge of the upper capacitor oscillates with an amplitude around the average value equal to Over half the oscillation period, it decreases from the maximum value at the initial moment to zero, when all the charge is on the lower capacitor.
Expression (26) for the oscillation frequency, of course, could be written right away, since in the circuit under consideration the capacitors are connected in series. However, it is difficult to write expressions (34) directly, since under such initial conditions it is impossible to replace the capacitors included in the circuit with one equivalent one.
A visual representation of the processes occurring here is given by the mechanical analogue of this electrical circuit, shown in Fig. 163. Identical springs correspond to the case of capacitors of the same capacity. At the initial moment, the left spring is compressed, which corresponds to a charged capacitor, and the right one is in an undeformed state, since the analogue of the capacitor charge here is the degree of deformation of the spring. When passing through the middle position, both springs are partially compressed, and in the extreme right position the left spring is undeformed, and the right one is compressed in the same way as the left one at the initial moment, which corresponds to the complete flow of charge from one capacitor to the other. Although the ball undergoes normal harmonic oscillations around its equilibrium position, the deformation of each of the springs is described by a function whose mean value is nonzero.
Unlike an oscillatory circuit with one capacitor, where during oscillations a repeated half-recharge occurs, in the system under consideration the initially charged capacitor is not completely recharged. For example, when its charge is reduced to zero, and then restored again to the same polarity. Otherwise, these oscillations do not differ from harmonic oscillations in a conventional circuit. The energy of these oscillations is conserved, if, of course, the resistance of the coil and connecting wires can be neglected.
Explain why, from a comparison of formulas (1) and (2) for mechanical and electromagnetic energies, it was concluded that the analogue of stiffness k is and the analogue of mass is inductance and not vice versa.
Give a rationale for deriving expression (4) for the natural frequency of electromagnetic oscillations in the circuit by analogy with a mechanical spring oscillator.
Harmonic oscillations in a circuit are characterized by amplitude, frequency, period, phase of oscillations, and initial phase. Which of these quantities are determined by the properties of the oscillatory circuit itself, and which depend on the method of excitation of oscillations?
Prove that the average values of electric and magnetic energies during natural oscillations in the circuit are equal to each other and constitute half of the total electromagnetic energy of oscillations.
How to apply the laws of quasi-stationary phenomena in an electrical circuit to derive the differential equation (12) of harmonic oscillations in the circuit?
What differential equation does the current in an LC circuit satisfy?
Derive an equation for the rate of decrease in oscillation energy at low damping in the same way as was done for a mechanical oscillator with friction proportional to the speed, and show that for time intervals significantly exceeding the oscillation period, this decrease occurs according to an exponential law. What is the meaning of the term “low attenuation” used here?
Show that the function given by formula (21) satisfies equation (16) for any values of and a.
Consider the mechanical system shown in Fig. 163, and find the dependence on the time of deformation of the left spring and the speed of the massive body.
A circuit without resistance with inevitable losses. In the problem considered above, despite the not entirely ordinary initial conditions for charges on capacitors, it was possible to apply ordinary equations for electrical circuits, since the conditions for quasi-stationary processes were met there. But in the circuit, the diagram of which is shown in Fig. 164, with formal external similarity to the diagram in Fig. 162, the quasi-stationary conditions are not satisfied if at the initial moment one capacitor is charged and the second is not.
Let us discuss in more detail the reasons why the conditions of quasi-stationarity are violated here. Immediately after closing

Rice. 164. Electric circuit for which quasi-stationary conditions are not met
key, all processes take place only in capacitors connected to each other, since the increase in current through the inductor occurs relatively slowly and at first the branch of the current into the coil can be neglected.
When the key is closed, fast damped oscillations occur in a circuit consisting of capacitors and the wires connecting them. The period of such oscillations is very short, since the inductance of the connecting wires is low. As a result of these oscillations, the charge on the capacitor plates is redistributed, after which the two capacitors can be considered as one. But this cannot be done at the first moment, because along with the redistribution of charges, a redistribution of energy also occurs, part of which turns into heat.
After the fast oscillations decay, oscillations occur in the system, as in a circuit with one capacitor, the charge of which at the initial moment is equal to the initial charge of the capacitor. The condition for the validity of the above reasoning is the smallness of the inductance of the connecting wires compared to the inductance of the coil.
As in the problem considered, it is useful to find a mechanical analogy here. If there two springs corresponding to capacitors were located on both sides of a massive body, then here they should be located on one side of it, so that the vibrations of one of them could be transmitted to the other when the body is stationary. Instead of two springs, you can take one, but only at the initial moment it should be deformed non-uniformly.
Let's grab the spring by the middle and stretch its left half to a certain distance. The second half of the spring will remain in an undeformed state, so that the load at the initial moment is displaced from the equilibrium position to the right by a distance. Under the initial conditions of our problem, when half of the spring is stretched by a distance, the energy reserve is equal to , as is easy to imagine, the stiffness of “half” of the spring is equal to If the mass of the spring is small compared to the mass of the ball, the frequency of natural oscillations of the spring as an extended system is much greater than the frequency of oscillations of the ball on the spring. These “fast” oscillations will die out in a time that is a small fraction of the period of the ball’s oscillations. After the fast oscillations attenuate, the tension in the spring is redistributed, and the displacement of the load remains practically equal since the load does not have time to move noticeably during this time. The deformation of the spring becomes uniform, and the energy of the system equals
Thus, the role of rapid oscillations of the spring was reduced to the fact that the energy reserve of the system decreased to the value that corresponds to the uniform initial deformation of the spring. It is clear that further processes in the system do not differ from the case of uniform initial deformation. The dependence of the displacement of the load on time is expressed by the same formula (36).
In the example considered, as a result of rapid vibrations, half of the initial supply of mechanical energy was converted into internal energy (heat). It is clear that by subjecting not half, but an arbitrary part of the spring to initial deformation, it is possible to convert any fraction of the initial supply of mechanical energy into internal energy. But in all cases, the oscillation energy of the load on the spring corresponds to the energy reserve for the same uniform initial deformation of the spring.
In an electrical circuit, as a result of damped fast oscillations, the energy of a charged capacitor is partially released in the form of Joule heat in the connecting wires. With equal capacities, this will be half the initial energy reserve. The second half remains in the form of energy of relatively slow electromagnetic oscillations in a circuit consisting of a coil and two capacitors C connected in parallel, and
Thus, in this system, idealization in which the dissipation of oscillation energy is neglected is fundamentally unacceptable. The reason for this is that rapid oscillations are possible without affecting the inductor or massive body in a similar mechanical system.
Oscillatory circuit with nonlinear elements. When studying mechanical vibrations, we saw that vibrations are not always harmonic. Harmonic oscillations are a characteristic property of linear systems in which
the restoring force is proportional to the deviation from the equilibrium position, and the potential energy is proportional to the square of the deviation. Real mechanical systems, as a rule, do not possess these properties, and vibrations in them can be considered harmonic only for small deviations from the equilibrium position.
In the case of electromagnetic oscillations in a circuit, one may get the impression that we are dealing with ideal systems in which the oscillations are strictly harmonic. However, this is true only as long as the capacitance of the capacitor and the inductance of the coil can be considered constant, that is, independent of charge and current. A capacitor with a dielectric and a coil with a core, strictly speaking, are nonlinear elements. When a capacitor is filled with a ferroelectric, i.e., a substance whose dielectric constant strongly depends on the applied electric field, the capacitance of the capacitor can no longer be considered constant. Similarly, the inductance of a coil with a ferromagnetic core depends on the current strength, since the ferromagnet has the property of magnetic saturation.
If in mechanical oscillatory systems the mass, as a rule, can be considered constant and nonlinearity arises only due to the nonlinear nature of the acting force, then in an electromagnetic oscillatory circuit nonlinearity can arise both due to a capacitor (analogue of an elastic spring) and due to an inductor ( analogue of mass).
Why is the idealization in which the system is considered conservative not applicable for an oscillatory circuit with two parallel capacitors (Fig. 164)?
Why are rapid oscillations leading to dissipation of oscillation energy in the circuit in Fig. 164, did not occur in a circuit with two series capacitors shown in Fig. 162?
What reasons can lead to non-sinusoidal electromagnetic oscillations in the circuit?
Characteristics of men


